Deep Learning Architectures for Imaging Problems

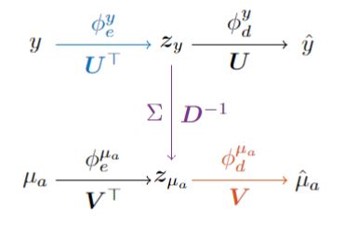
In the last decade, Deep Learning techniques have experienced huge improvements, both on the technological side and on the theoretical side. Generative Adversarial Networks (GANs) are widely used for the generation of synthetic but realistic images. These networks are trained by inducing two different architectures, namely the generator and the discriminator, to "race" one against the other: the generator tries to create realistic images, whilst the discriminator has to determine if the data taken as input is a natural or a synthetic image. The creation of such GANs requires a suitable design of the architecture and the choice of a well--tailored loss function for the training. Among their natural application, as the generation of synthetic leaf images for the training of a Neural Network for automatic disease segmentation, GANs can be used in Deep Image Prior (DIP) approaches or in Neural Blind Deconvolution (NBD) problems. In biomedical imaging, particularly in Diffuse Optical Tomography (DOT) frameworks, Neural Networks can be trained to generalize the Singular Value Decomposition (SVD) of linear operators: they take hence the name of Learned-SVD. These architectures consists namely in two autoencoders: considering the classical SVD of a matrix J=UDV^t, one autoencoder mimics the action of U^t and U, while the other mimics the action of V^t and V. Hence, the two latent spaces are connected by an operator which plays the role of the singular values.

Stochastic optimization for data-driven methods

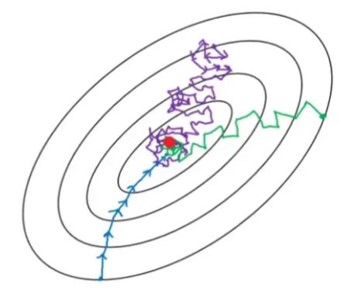
Two main factors have mainly contributed to the development of data-driven methodologies in recent years. Firstly, the ongoing development of hardware accelerators such as GPUs and FPGAs has enabled the employment of increasingly larger models within shorter time frames. Secondly, the increasing digitization of everyday life has simplified and amplified data collection, resulting in a substantial amount of data being readily accessible for processing. Undoubtedly, the large availability of data is the primary advantage of data-driven methods; however, managing huge datasets leads to significant challenges. The need to handle huge datasets together with models characterized by many parameters makes stochastic optimization an essential tool. In recent years, many researchers belonging to the OASIS group started to investigate stochastic optimization models and their relative numerical methods. The aim is twofold: to generalize effective approaches employed in the deterministic framework to the stochastic setting and to design new efficient schemes specifically tailored for tackling stochastic minimization problems. Particular attention is devoted to algorithms suitable to be exploited in deep learning applications.

Optimization for real medical imaging

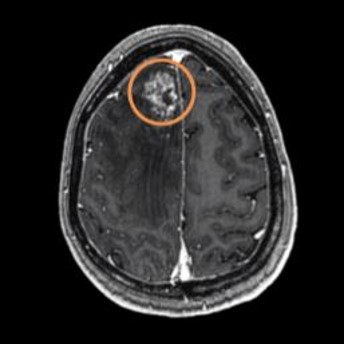
Medical imaging is a central part of the improved outcomes of modern medicine. In medical imaging, inverse problems arise whenever we seek to reveal internal structures (hidden by the skin and bones) but we have only indirect (and often just a few) measurements of an anatomical region of interest, or whenever the digital image is corrupted by strong artifacts and noise. Successfully solving the corresponding imaging problem, therefore, requires algorithms specifically designed for each task and kind of imaging. Ongoing research topics are (i) volumetric reconstruction of MRI or X-ray tomographic images from subsampled measurements; (ii) denoising and deblurring of images affected by specific artifacts, depending on the acquisition geometries, and by mixed noise with statistics due to different noise sources; (iii) mathematically grounded image processing to enhance anatomic details, as in contrast agent or dual energy imaging. All these tasks are modeled as large-scale inverse problems. Optimization strategies are used to achieve high-quality and reliable medical images, solving regularized constrained problem formulations with fast iterative algorithms, eventually powered by deep-learning neural networks. For years, Oasis members have also been collaborating with Italian and multinational companies, leaders in biomedical manufacturing. Several partnerships have started to develop software, making state-of-art algorithms and techniques fit specific requirements and needs of clinical settings.

Variational methods for imaging

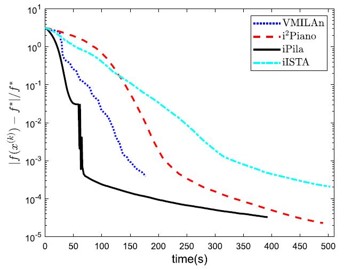
Several tasks in image processing, including image restoration, image inpainting, image super resolution, blind deconvolution and others, are typically formulated as composite optimization problems, where the objective function is the sum of a data fidelity function, measuring the distance between the unknown object and the acquired data, plus some regularization terms or constraints, aimed at imposing some prior knowledge on the object itself. The numerical solution of these problems requires effective optimization strategies able to handle possible non-convex and non-differentiable terms, while retaining a low computational cost per iteration. In this context, proximal splitting methods have become attractive in the past few years. These methods proceed by splitting the objective function as the sum of two or more terms, and then involve each (or some of the) terms by evaluating its proximal operator. Despite their simplicity, standard implementations of these methods exhibit a slow rate of convergence towards the solution, so that acceleration techniques are required in order to improve their numerical performance. In this stream of research, we design efficient proximal splitting methods suited for composite optimization problems arising in signal and image processing. These newly designed methods will combine classical strategies in optimization (e.g. inertia, line-searches, variable metrics) with more recent techniques (e.g. unrolling, plug-and-play) in novel and smart ways. On the one hand, we will deepen the theoretical analysis of these methods, ensuring convergence under different settings. On the other hand, we will apply the proposed methods to difficult imaging applications arising in medicine and microscopy. We will also employ our methods to address novel deep learning approaches arising in image restoration, including for instance the very recent Deep Image Prior, which relies on the implicit regularization provided by representing images as the output of generative Convolutional Neural Network (CNN) architectures.